Cleaning the house while the children are growing is like shoveling the driveway while it’s still snowing.
A framed needlepoint of this adage adorned the wall of our kitchen as I was growing up and its message occupied my thoughts as I shoveled our New England driveway for the third time in just over a week. What was I doing, shoveling as the snow fell? Did I expect to win this race with Mother Nature or was the snow just piling up at a slightly slower rate due to my efforts to remove it? Questions like these exist in the province of systems thinking, and in SageModeler represent a classic example of how dynamic modeling can help explore answers to them.
As I shovel, my focus is upon the accumulating snow in the driveway. Is it building up as I shovel, or diminishing over time? At any given moment I could measure the snow and use a collection of these measurements to see whether or not my effort was worthwhile. I’m currently just “eyeballing” it, though I could use a yardstick to be more precise. In a dynamic model built with SageModeler the deepening snow would be represented by a special “accumulating variable” called a collector. Collectors are essentially tubs, or bins, into which something can accumulate.
My current snowfall problem is more than mere accumulation, though. The storm is dropping snow at a certain rate. I am removing it with a certain number of shovelfuls every minute. Will I prevail? Do I need to shovel faster to make progress? Should I just forget all of this and buy a snowblower?
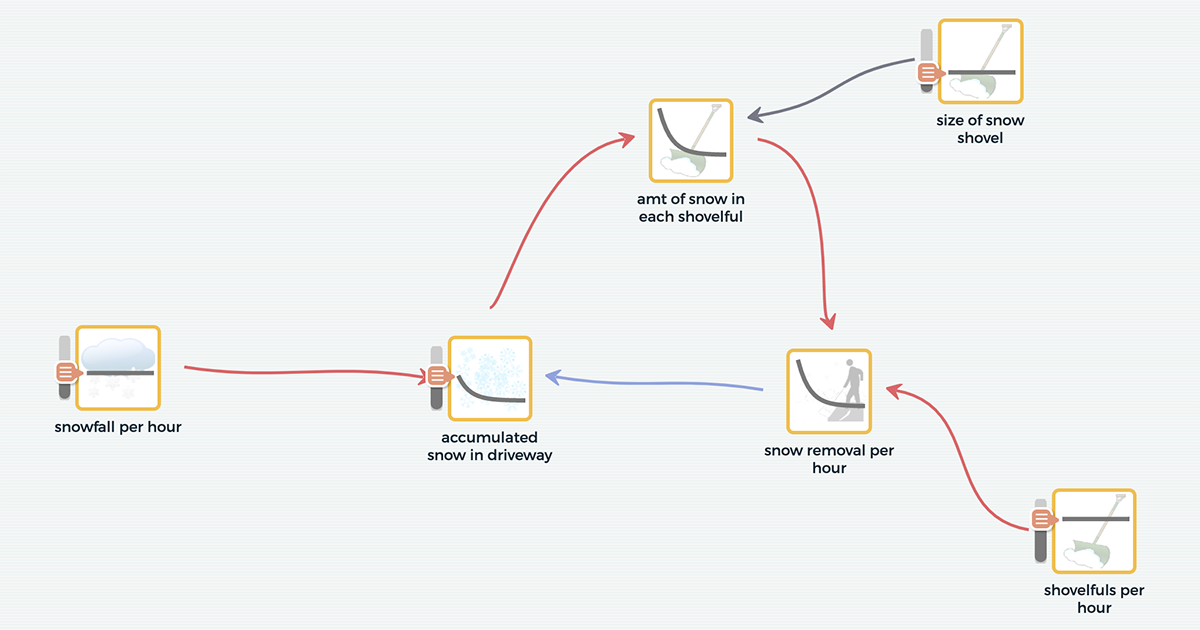
SageModeler time-based dynamic model of snowfall removal with “Accumulated snow in driveway” as a collector. Open the model, click the SIMULATE button, and change the independent variables. Watch as graphs are made inside each variable over time.
Dynamic models hold questions like these at the core of their structure. As modelers we are most often concerned with changes in accumulations that can be observed as time passes. We can investigate both huge questions—“Is there anything that humanity can do to prevent the rise of CO2 in the atmosphere?” or “What will happen to the number of humans migrating as global temperatures increase?”—and smaller ones—“How often do I need to fill my bird feeder?” or “When is it fruitless to shovel my driveway?”—by looking at changes in the accumulation of something over time.

While shoveling my driveway, I use mental calculation to determine whether or not I’m making progress. In dynamic modeling programs like SageModeler, a strict protocol is followed as calculations are made to create a possible future based on current conditions and assumptions. (In SageModeler, students don’t need to use any mathematics; all calculations are done “under the hood.”) To begin, the computer assesses the current “state” of the system, looking for and recording the current values in each collector. In the example of my driveway, it is a question of how much snow is currently on the ground.
Another important piece of information is the current rate of snowfall, or inflow, into the collector. In the real world, this is beyond my control, subject to the whims of nature, but in a model it might be represented as an independent variable and controllable by the modeler as she experiments with model simulation. The rate of snow removal, or outflow, is also specified and variable depending upon my store of energy, my desire to shovel, or even the size of the shovel I use.
In order to calculate snow amounts into the future, the computer combines all of the known information, starting with the current accumulation, adding to it the amount of new snow falling in a given time period and subtracting the amount shoveled away in the same period of time. The result is a new “state” or value for the accumulation of snow in the driveway.
What if there were some feedback in this system? Could it be that the amount of snow in the driveway affects the rate at which it is removed? For example, if the snow is deep, more snow can be lifted with each shovelful (to a limit, of course), and if I am indeed removing snow more quickly than it is falling, there will be diminishing volumes in each shovelful as I continue.
In the model, calculations begin with the current state of things as represented by the values of the collectors. The amount of snow presently in the driveway is used to determine how much snow is available to be removed during the time that elapses until the next determination of accumulation is recorded. If I’m winning the race with Mother Nature and removing snow faster than it is accumulating, every subsequent time period will offer a little less snow to the shovel, and over time the rate of snow removal will decline. This assumes that the actual rate at which the shoveling motion occurs does not change. (In the model above, I’ve added some variables and connections that take into account the declining amounts of snow available to the shovel as the shoveling continues.)
In summary, SageModeler calculates change over time by first recording the values of all collectors (accumulations) in the model. These values are then used to compute other calculable components in the model and then, together with all independent variables, are combined to calculate the rates at which the collectors will change during the next time period. The calculated inflow and outflow rates are then integrated into the previous collector value to calculate a new value at the next point in time.
You might well imagine that the time period chosen for these calculations—every second, minute, week, or year—might make a difference in how the model behaves. If I were to build a model that calculated snow removal from my driveway but only recalculated the accumulations once every week, a lot of information will have been lost in the interim. (I’ll explore this topic in an upcoming blog post.)
Over and over the computer makes these calculations, just as over and over I lift and throw each shovelful of snow over my shoulder. I imagine my mother inside the house, standing at the window, warm and watchful. She looks at the framed adage about cleaning the house that hangs on the kitchen wall, glances out at me as I shovel, and smiles. I smile, too.