Our Multilevel Computational Modeling collaborative project with Michigan State University has developed a novel theoretical framework based on a literature review of modeling, systems thinking (ST) and computational thinking (CT). The framework, which was also informed by years of work developing our SageModeler systems modeling software and researching student modeling, highlights how both ST and CT are involved in the process of modeling phenomena or problems.

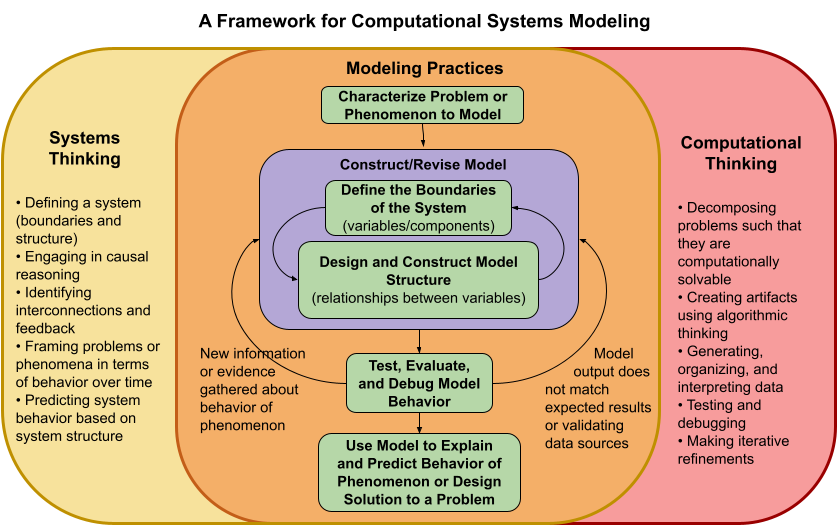
The center set of boxes describes five modeling practices and the cyclic nature of the modeling process (represented by the arrows). Engagement in each practice requires aspects of systems thinking and computational thinking.

Imagine that you want to study something with lots of interrelated factors, such as the effect of a vaccination program on an epidemic. There’s a lot to consider in the system—the effectiveness of the vaccine, the number of vaccinations administered, how infectious the virus is, the chance of being contacted by someone who is infected, and on and on. What happens if the vaccine is effective but few people are vaccinated, or vice versa? What happens if the infectivity of the disease changes over time?
It’s clear that the number of interactions in the system will quickly outpace our ability to mentally predict the system’s behavior, especially if we need to consider time delays and feedback.

In another example of a complex system, there are multiple factors that affect the accumulation of CO₂ in the atmosphere, some that increase it (e.g., emissions from cars and factories, decaying organic matter) and some that decrease it (e.g., CO₂ absorption by the oceans, the growth of trees). Each of these factors has varying rates, with some dependent on the others. What does that mean for the effects on climate change?

In these cases, systems thinking is critical but may be insufficient to investigate solutions to complex problems.

To model these phenomena successfully, we also need computational thinking—the ability to apply logical and algorithmic thinking. By identifying patterns in phenomena, computational thinking helps us calculate the effect of the relationships between components of a system so that we can better predict phenomena. Although a computer is not required to engage in computational thinking, a computer’s processing speed is often necessary for exploring complex problems.

Thus, to fully explain complex phenomena or solve problems using models requires both systems thinking (ST) and computational thinking (CT). ​​The “Framework for Computational Systems Modeling” elucidates the synergy between modeling, ST, and CT.

We postulate that this framework can (a) guide curriculum developers and teachers in integrating ST and CT in the context of modeling in multiple STEM courses, (b) assist software developers and curriculum designers in developing effective learning tools and pedagogical supports that involve learners in modeling, ST, and CT, and (c) help researchers and teachers in measuring learners’ understanding and application of modeling, ST, and CT.

Learn more about our framework in a new article in Instructional Science. We describe the framework and associated aspects of ST and CT in each modeling practice by illustrating how the ST and CT aspects support the modeling process and we share examples of models to illustrate how ST and CT are integrated in and support the modeling practices. Like our SageModeler systems modeling tool and our curriculum, the article is free and open access, so it can be shared widely.