Last week, Paul, Ed, and I did physics. This is such a rare event that it deserves note. We actually developed a theory, collected data, compared theory to data, came up with new ideas and tested them. We only wish kids everywhere could have the same experience.
This investigation was prompted by Ewa Kedzierska’s presentation at the World Conference on Physics Education in Istanbul in early July*. She presented a student activity on bungee jumping that claimed that the jumper falls faster than a free-falling object. This seems difficult to believe, in spite of video data she presented—collected and graphed by the wonderful COACH software—that clearly showed this to be true. We immediately thought of many reasons why this should be impossible. Imagine jumping without a tethered Bungee cord—jumper and cord would fall in free-fall just as Galileo proved in his famous Tower of Pisa experiment (never mind the fatal consequences—this is physics!). Attaching the far end of the Bungee rope would seem to apply an upward force that could only slow the jumper, not speed her up!
As typical science skeptics, we had to do it ourselves and understand the mechanism, if the effect was true. Following the maxim that was current when CERN supposedly found neutrinos travelling faster than light—“Extraordinary results require extraordinary evidence”—we needed to do the experiment ourselves and get a feel for the situation. So Ed gathered a stepladder, chain (substitute Bungee), tennis ball (for the jumper), and a camera that takes 240 frames per second, and we collected data.
Paul, ever the theoretician, showed that the far end of a horizontal chain link held steady at the near end would fall faster than a free body, and hence, could impart some force to the falling chain. Thus, each chain link, on reaching the bottom of the “U” formed by the falling links, could impart a bit of force on the falling side and make it fall faster than free-fall. Another way of saying this is that each link, when brought to a halt, rotates 180 degrees and can exert some torque on the falling side.
We collected the data, and clearly saw the effect. It is real! And it is huge when the falling mass is small. We photographed side-by-side tennis balls, one attached to a chain and one in free fall. The one with the chain fell faster! Every time. The picture shows a frame from a movie of the experiment, clearly showing Paul about to fall (he didn’t), and the free-falling ball going slower.
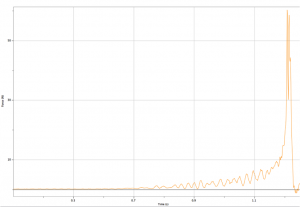
Don’t believe us? Do it yourself. We attached a force sensor to the end of the chain and could detect the force from individual links. The force increased non-linearly and dramatically. Stopping the last link required 50 N even though the entire chain weighed only 4 N (see graph). We are still arguing about why the force increases so much for the last few links.
I noticed that sometimes if the falling part of the chain is close to the tethered part, the links at the bottom of the “U” do not rotate, but slide. When they slide, they do not rotate and, hence, should not accelerate the falling chain. We could hear the difference, but our results were inconclusive, because near the end of the fall, the chain doesn’t fall evenly and this causes it to revert to the link-rotation mode.
In our next blog, we’ll present the data and our analysis. Stay tuned.
* Published in Physics Education 45(1), pp 63-72 (2010).
6 thoughts on “Bungee Physics”
Comments are closed.
You are killing me….wow, I wish I had been there. This is going into my bag of tricks this year, for sure. I’m not sure if I have a physics student or not this semester but sometime this year I will..
BW
Hey, great to hear from you Brad. Glad you liked it. I have to credit Ton Ellemeijer, his wife Ewa, and André Heck who popularized this problem in Holland. You remind me that I should post my analysis of this problem, which turns out to also be in the literature.
Your work has sparked a debate on facebook. While it is easy to see the appreciable acceleration with the chain attached, as opposed to free fall, may I suggest that the acceleration is due to centrifugal force acting at the middle of the chain when it becomes stationary?
We may be talking about the same phenomenon but using different language. I don’t much care for the term “centrifugal force,” which doesn’t, strictly speaking, exist except in accelerated reference frames, but insofar as rotational acceleration of the links is important it does sometimes help to think of the link as “trying” to move in a straight line and exerting a force, rather than the consistent but a bit counter-intuitive explanation of a force being exerted on the link that’s making it do something it wouldn’t ordinarily do (i.e., accelerate).
One way to convince yourself that the effect is real is to think about the motion of a uniform massive bar suspended at one end on a frictionless pivot and acted upon by gravity so that it rotates about the pivot. The rotational acceleration, alpha, is the torque divided by the moment of inertia of the bar about one end. If the length of the bar is L and its mass is m then the torque is 1/2 m g L (since gravity can be taken as acting on the center of mass which is 1/2 L distant from the pivot point) and the moment of inertia is 1/3 m L^2. This gives an acceleration of the center of mass of 3/4 g (it’s less than g because of the upward force exerted by the pivot) and an acceleration of the tip of 3/2 g.
So the tip, in the absence of any other force, naturally accelerates faster than g. Now if you add in the rest of the chain the acceleration goes down, but it doesn’t go down all the way to g.
By the way, you say that this blog post has generated some discussion on Facebook? How interesting! Could you point us to that discussion?
Thanks,
Paul
Hi,
I’ve looked through your blog posts and cannot find the one that you said you were going to post about your data and analysis. Is there any way you could provide me with this information or possibly a more detailed write-up of your procedures? I am considering doing an experiment like this for my IB Physics class and your investigation seems to be the closest thing I can find to what I would like to do.
Thank you,
Annalise
As you may have surmised, Annalise, we never did get around to writing that follow-up blog — mainly, I guess, because we all got busy and failed to carry through the analysis. I do have some notes somewhere that I started. I don’t remember how complete they are, but if I can find them and they’re in decent shape, I’ll write them up and post them here.