Constructive Chemistry: A Case Study of Gas Laws
Science should be taught as a verb as well as a noun. Performing science is a compelling and effective way to learn. It is through the process of exploration, creation, and invention that theories are applied, ideas are tested, and knowledge is synthesized and advanced.
Teaching by engaging students in creating their own artifacts can be traced to Seymour Papert’s advocacy of Logo through its offspring AgentSheets, StarLogo, NetLogo, Scratch, Squeak, and others. By creating animations and games with these tools, students are enticed to learn core mathematical and programming concepts and apply them to their creations. In physics, Interactive Physics and the recently released Phun and Crayon Physics, with which students can easily create physics-based simulations that model the real world, have shown great potential in teaching Newtonian mechanics. This will greatly help them prepare for any major science exams in college. Furthermore, finding the right study material on https://examgenius.org is also one factor to ace any science exams.
Our Molecular Workbench (MW) software can be used in a similar way. Unlike the tools mentioned above, MW is specialized to model electrons, atoms, and molecules, which makes it applicable across physics, chemistry, biology, and engineering. Interactive simulations produced with MW allow students to learn through exploration and inquiry. Students can also learn by creating their own simulations that show emergent behaviors under various conditions. As students create simulations, they learn important concepts in science, how those concepts are connected, and how to apply them to design working systems.
Because the Molecular Workbench simulation engine calculates the motion of atoms and molecules based on their interactions, it can model a considerable depth and breadth of science. With this versatility and a graphical user interface for creating simulations, MW is perfectly suited for educators interested in exploring the constructionist approach of teaching science with computer simulation tools.
Over the last two years, we have collaborated with chemistry professor Neocles Leontis at Bowling Green State University (a science teacher preparation institution in Ohio) to pilot test the constructionist strategy in his physical chemistry course. The results may provide lessons for the wider adoption of this pedagogy.
Digging more deeply into the gas laws
Professor Leontis challenged his students to answer questions by designing molecular simulations. One of the challenges concerns the Ideal Gas Law: PV=NkBT, where P is the pressure, V is the volume, N is the number of molecules, kB is the Boltzmann constant, and T is the absolute temperature. Professor Leontis posed a number of questions that he would not have been able to ask his students before, because without high-level analytical skills involving advanced mathematics or computation, the questions can’t be easily answered. But because Molecular Workbench is a tool for solving complex problems with just a few mouse clicks, he did not have to worry about his students’ mathematical backgrounds. He was confident that they could answer his questions using MW simulations.

Why must N be the number of molecules?
The first challenge asked students to think about why N has to be the number of molecules instead of the number of atoms. To answer this question, a student compared two containers that had the same number of atoms, but in one container she created a covalent bond between every two atoms (Figure 1). Thus, she produced a gas of diatomic molecules and reduced the number of freely moving entities to half.
Running the simulation for a while, she observed that the volume of the gas in the right container decreased to about half the volume of the gas in the left container. A careful observation of the simulation immediately revealed why. As the two atoms of a molecule move together, when one of them bounces off the piston, the other has a high probability of being towed away without hitting the piston. As a result, the frequency with which atoms collide with the piston decreases by half.
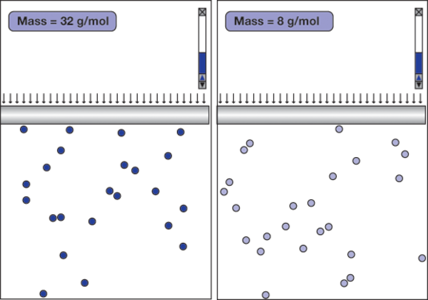
Does the mass of the molecules affect the gas law?
Figure 2 shows a student’s simulation designed to investigate this question. The gas in the left container (A) is composed of atoms that are three times more massive than the atoms of the gas in the right container (B). The simulation shows that under the same external pressure and temperature, the volumes of both gases turn out to be about the same after they reach equilibrium. This means that the average volume an atom occupies depends only on the pressure and the temperature, even though the atoms in A appear to move at an average speed that is only half that of the atoms in B. This is quite a surprising result!
How do atoms of different masses “know” to keep their distance? The answer can be found by observing the collisions of the atoms with the pistons. Each collision of an atom with the piston in A delivers an average impulse that is twice as much as each collision of an atom with the piston in B. In order for the gases to have the same pressure, the frequency of the atom-piston collisions in A must be half of that in B. Considering that the atoms in A move half as fast, the only way to keep the frequency of the atompiston collisions in A half that in B is to keep the density of atoms—hence the volume—the same.
Can you break the Ideal Gas Law?
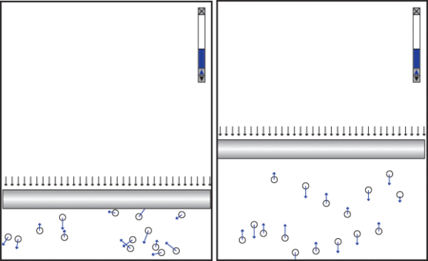
Students are often motivated by the challenge to design something that violates a physics law. They are inspired to use their creativity. One student designed a subtle experiment in which all the atoms in one container moved perpendicular to the piston while the atoms in another container moved in all directions with an initial setup that guaranteed the equipartition of kinetic energy in each direction (Figure 3).
After running his simulation, he wrote, “I found out that the volume of the particles that are moving in 1D is larger than the volume of the particles moving in 2D even though they all have the same speed. I assume, however, since momentum is conserved, that the net speeds in both simulations are the same, but the difference is that in the 1D model, all the momentum is in the y-direction. Let’s call all of this momentum P. In the 2D model, half of the momentum is conserved in the x-direction (P/2) while the other half is conserved in the y-direction (P/2), which leads me to believe that the 2D model’s piston should have half the height as the 1D model’s piston.” Indeed, the simulation shows that the volume of the gas in the right container is approximately half that of the gas in the left container. Is the Ideal Gas Law broken? We leave the answer to you.
Concluding thoughts
Although this pilot test was done with college students, there is nothing to prevent high school teachers from trying this constructionist pedagogy. A unique strength of Molecular Workbench is that it permits teachers to scaffold a challenge activity to help students design their own simulations. For example, Professor Leontis put two identical models side by side on a page and asked students to modify one so that it would exhibit a different behavior of scientific significance. This scaffolding design ensures that students will not be intimated by the complexity of the software and lowers barriers for student engagement.
The simulations created by Bowling Green students indicate that students can learn important ideas when they use their imagination and create their own simulations to solve challenges. Indeed, some of their simulations reveal solutions that even we had not considered. As Albert Einstein said, “Imagination is more important than knowledge. For knowledge is limited to all we now know and understand, while imagination embraces the entire world, and all there ever will be to know and understand.” These students have proven Einstein’s assertion and we are grateful for their insights about gas laws and how we should teach them.