Engaging in Computational Thinking Through System Modeling

What is the effect of reintroducing wolves to Michigan’s Isle Royale National Park? How is CO₂ affecting our oceans and the organisms that live there? How can something that can’t be seen crush a 67,000 lb. oil tanker made of half-inch steel? Solving such questions requires thinking about the interrelated factors in a system: predators, prey, and various parts of a park ecosystem, for example, or carbon dioxide, acidity of the water, and shellfish health, and so on.

Most critical issues facing us today can be modeled as a complex system of interrelated components, involving chains of relationships and feedback between parts of the system. A common approach for understanding and solving problems such as these involves using a computer to simulate a model of the system. Developing and using system models requires computational thinking skills not only by the software engineers writing the code, but also by the entire team working to understand the system. A computational thinking perspective is necessary for everyone to contribute to decomposing the problem such that it can be modeled, tested, debugged, and used to understand the system under study. Indeed, the Next Generation Science Standards (NGSS) emphasize the importance of computational thinking and modeling using the lens of systems and system modeling.

Scaffolding Computational Thinking Through Multilevel System Modeling is a collaborative project with Michigan State University and the Concord Consortium funded by the National Science Foundation to explore how engagement in system modeling combines both systems thinking and computational thinking. Our goal is to investigate how students’ scientific explanations are informed by the computational thinking they use while developing system models, and how engagement in constructing system models may develop students’ computational thinking skills.

Contextualized framework for computational thinking

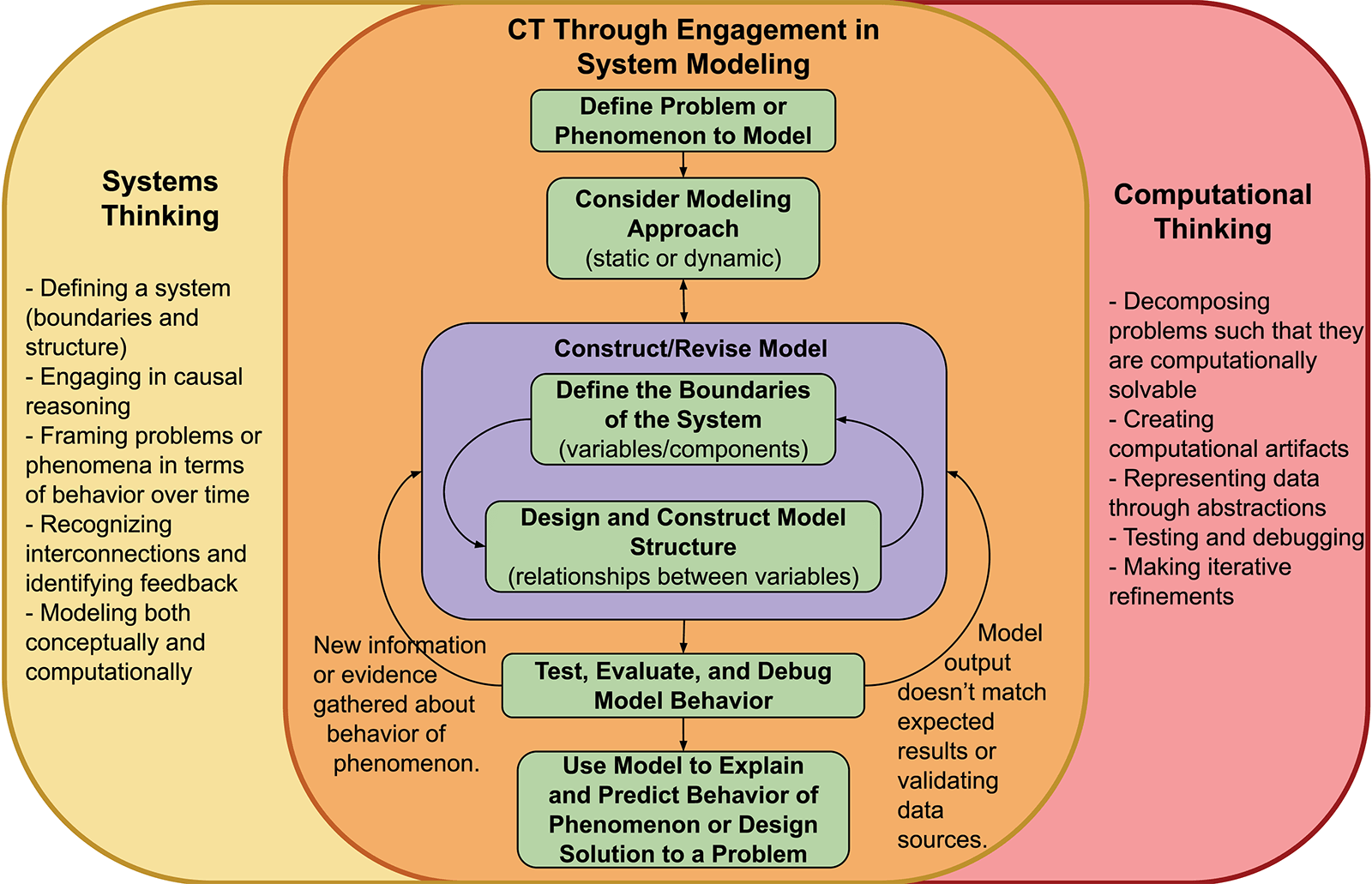
To guide our research, curriculum development, and teacher supports, we have developed a contextualized framework to illustrate how aspects of systems thinking (ST) and computational thinking (CT) overlap in the context of system modeling (Figure 1). In the diagram, systems thinking is presented on the left in yellow, computational thinking on the right in red, and the overlap contains the system modeling cycle in orange. Within system modeling, the set of green boxes describes the phases of system modeling; the arrows represent the cyclic nature of engaging in the modeling process. Each phase marries aspects of both ST and CT. For example, to define the boundaries of the system involves defining a system from ST and decomposing problems and representing data through abstractions from CT. While designing and constructing a system model, students can compare the model output to some known behavior of the system under study. In this way students apply modeling both conceptually and computationally from ST and testing and debugging from CT. Such integrations occur throughout the framework. We believe that the interplay of systems thinking and computational thinking during the process of system modeling can promote growth across all three areas.

Multilevel system modeling

Engagement in system modeling has been historically difficult for students. Two obstacles have hampered this approach in K-12 STEM education: 1) students must know how to code or write equations to define relationships in the model and 2) creating a computable system dynamics model requires students to draw upon elements of computational thinking and systems thinking they are not typically exposed to, including an understanding of the nature of feedback in complex systems.

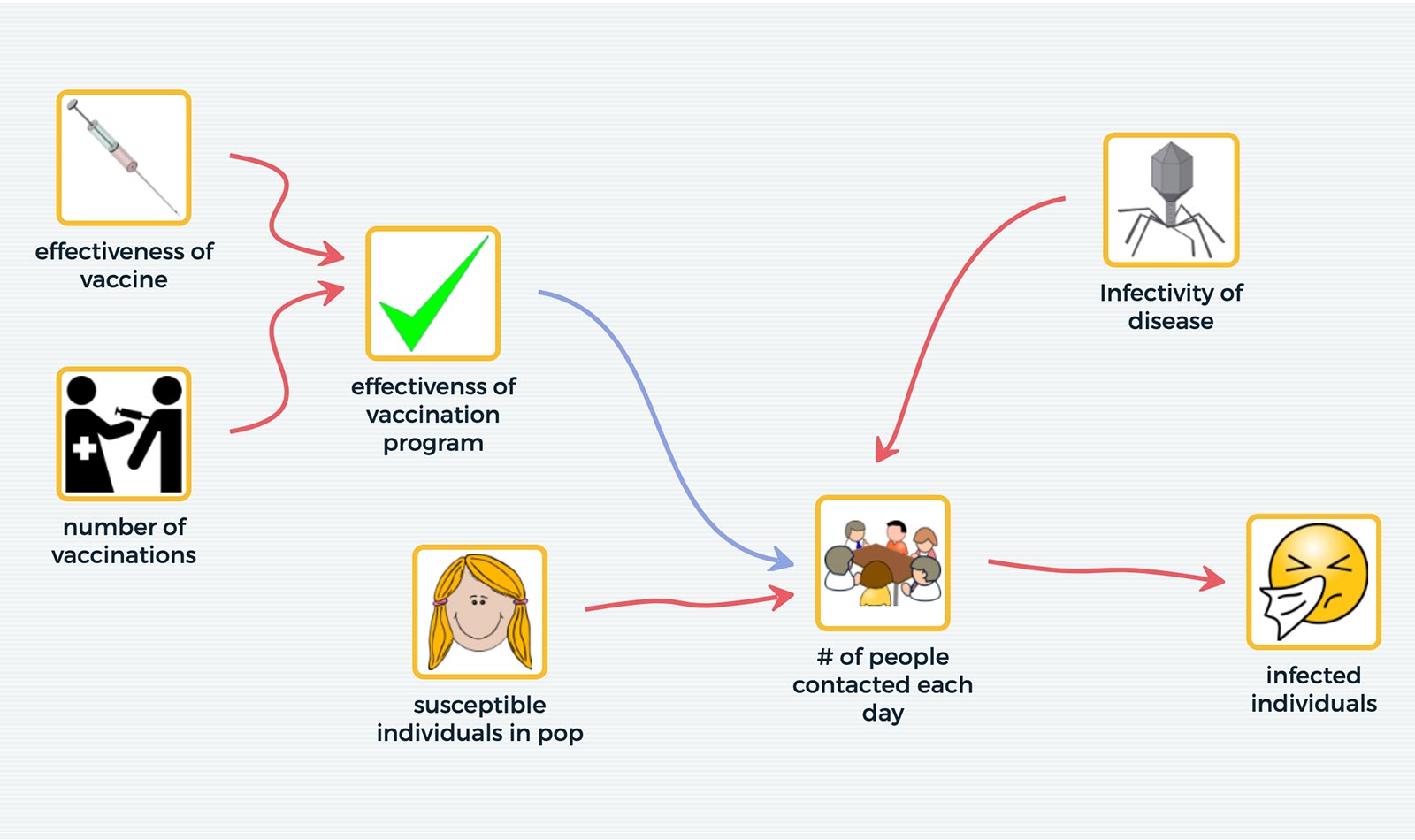
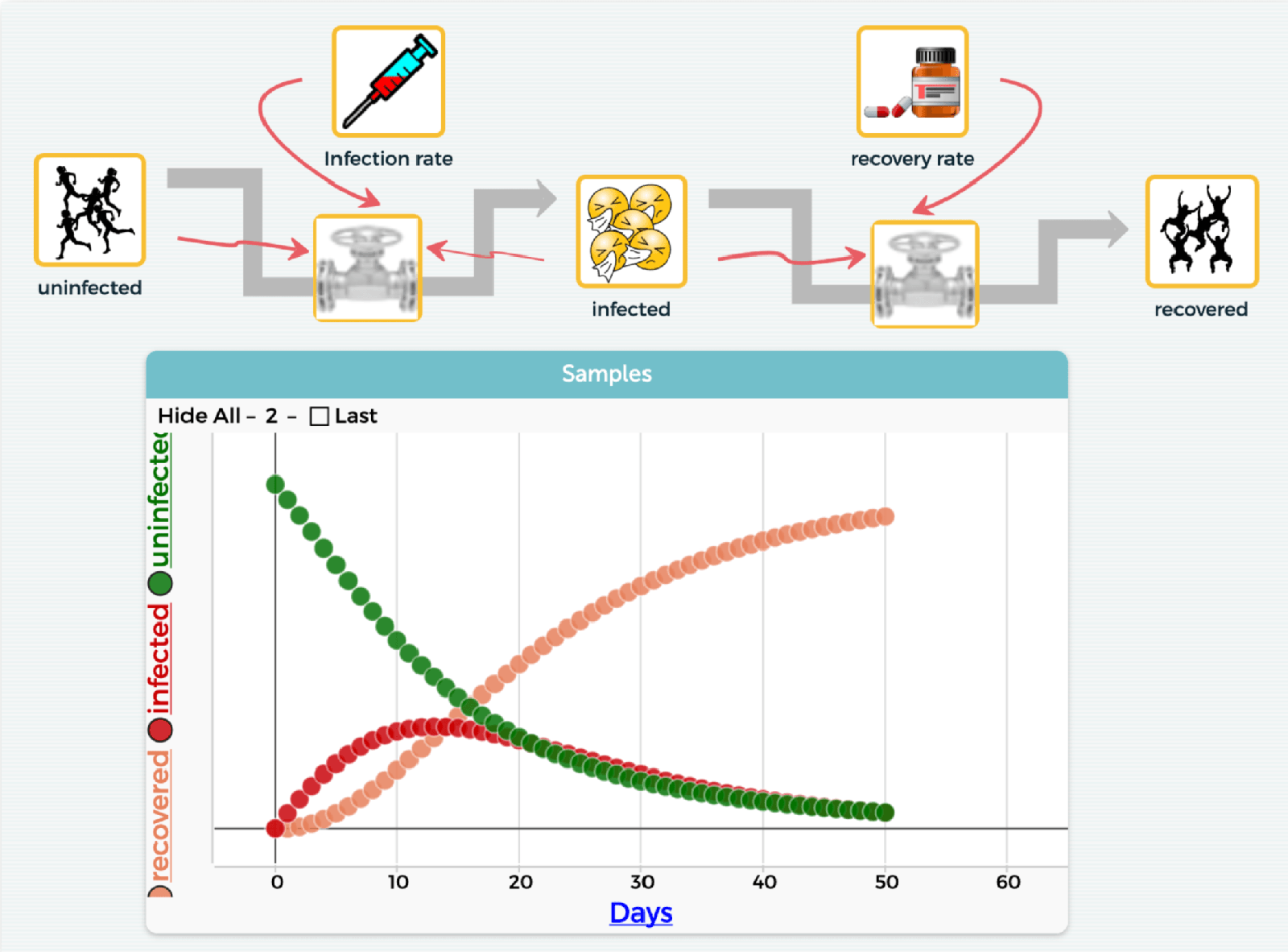
To overcome the first obstacle, we have been developing a system modeling tool called SageModeler, designed to provide an onramp to help students as young as middle school age design, create, and use system models. A simple drag and drop interface allows students to quickly select variables and define relationships between them, without requiring numbers, formulas, or coding. Quantities are represented on a scale of “low” to “high.” Students consider how a change in the value of variable A affects variable B. Using words, menu selections, and pictures of graphs, students define the functional relationships between variables, then run their system model to test ideas about how complex phenomena work.

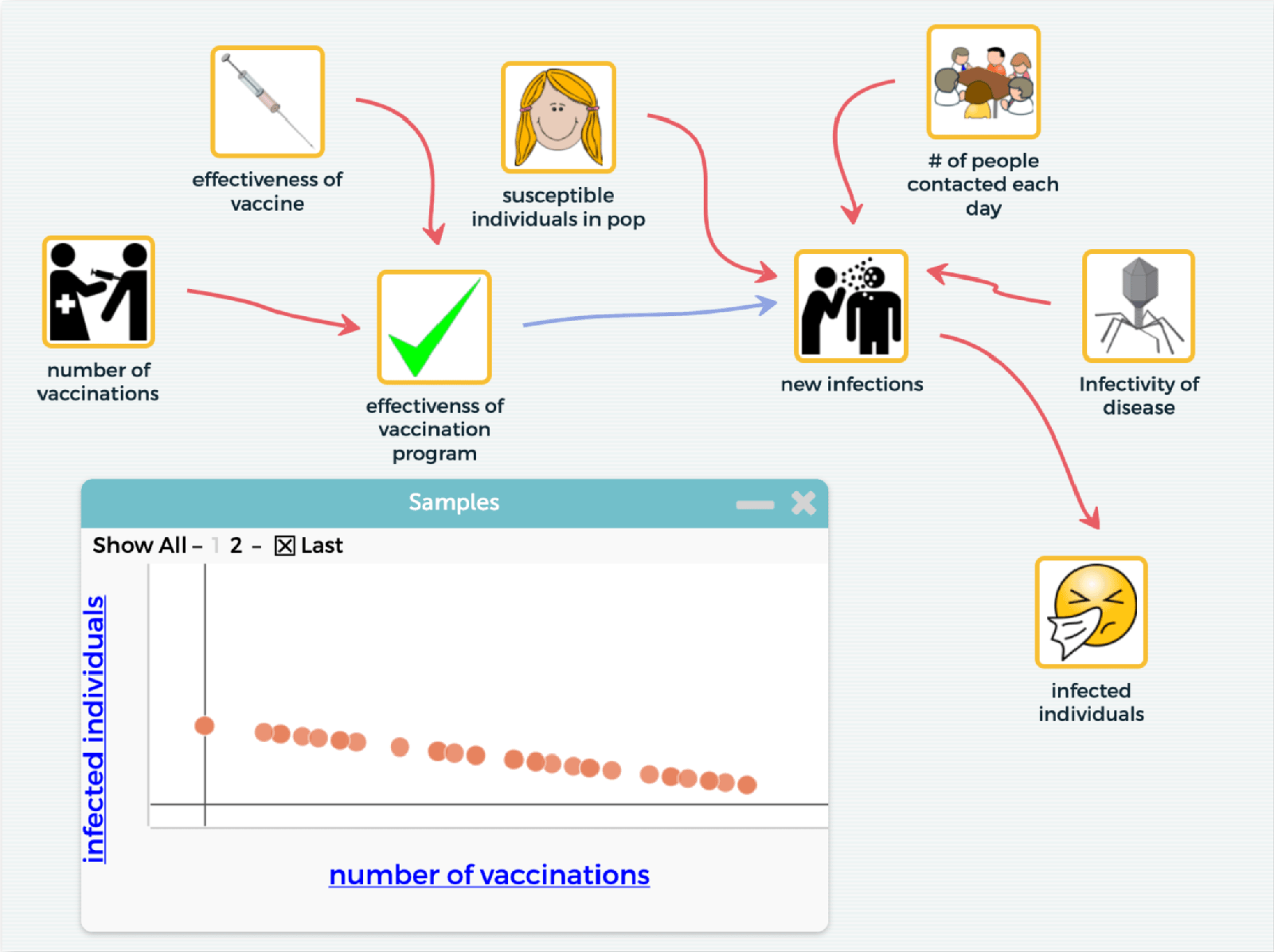
To address the second obstacle, we are exploring ways to scaffold students in the development of system dynamic models by focusing on key aspects of CT and ST as they relate to the modeling task. This scaffolding takes place both in the curriculum and within the affordances of the modeling tool. SageModeler supports three levels of complexity from model diagrams to static equilibrium models to time-based, system dynamics models (Figure 2).

Students can start with variables and links between them to form a system model diagram. As they include variables, they must consider the boundary of the system. Are the variables the right scale and scope for the phenomenon being modeled? Are the components of the model conceptualized as variables that can be calculated rather than just objects in the system? How do variables affect other variables? Even a simple model diagram provides rich opportunities for students to think about the system and begin engaging in both CT and ST.

To make the diagram into a runnable model, the relationship links between the variables need to be defined not just in direction, but in some semi-quantitative way. For example, in a model of climate change students might indicate that an increase in CO2 emissions from factories results in a proportional change in CO2 in the atmosphere. We call this a static equilibrium model where the effects of independent variables are instantly carried through the model, resulting in a new equilibrium state. With this kind of model the output can be compared with validating data sources to debug the model behavior and elicit revisions to better match real-world systems.

In system dynamic models, time can be introduced by defining one or more variables as “collectors” (traditionally known as “stocks” in system modeling). Students can also include feedback into the system and observe the behavior of the system over some defined time period. Because these models involve iterative calculations and can result in non-intuitive complex system behavior, especially when feedback is involved, we believe that this type of modeling provides the most opportunities for engaging in various aspects of both ST and CT. By moving from simpler to more complex modeling approaches, we hope to overcome the difficulties students have had with building runnable system dynamics models, to engage them in understanding complex phenomena, and to foster both computational and systems thinking skills and practices. Learning how to support this approach is at the heart of our research.

Research into computational thinking

The following questions guide our project research on student learning and teacher practice:

1) How are students’ scientific explanations informed by the computational thinking they engage in during iterative development of system models?

2) In what ways can curricular materials and technological tools best scaffold the development of students’ computational thinking and system modeling practices?

3) How can teachers scaffold the construction and simulation of computer models to more thoroughly engage students in computational thinking practices?

We are working with high school teachers in Massachusetts and Michigan to investigate these questions. We are collecting student modeling artifacts as well as their responses to embedded assessments within curriculum units, and supplementing these data sources with screencast videos, lab and classroom-oriented observations, exploratory instructional sessions with individual students, and interviews of both students and teachers.

Embedded assessments in online curricular materials are used to evaluate changes in students’ knowledge of disciplinary core ideas related to a particular phenomenon and their ability to construct and interpret explanatory models. After each iteration in which students build, test, share, and revise their models, they reflect on the state of their model and why they made any changes, and describe how well their model currently works to explain the phenomenon they are investigating. We log each iteration of the student model for post-analysis, including any tables and graphs of model output they created in SageModeler. Student models are analyzed for their ability to provide a causal account of the disciplinary phenomenon under study.

Screencasting software, which records student actions and audio from the computer microphone, serves to capture software usability issues, online curricular interactions and interpretations, and conversations among pairs of students while they are designing and testing their models. These screencasts allow us to explore how student modeling and computational thinking practices (especially testing, revising, and debugging) change over time. Interviews and longer exploratory instructional sessions probe student understandings of their models, how the models provide an explanation of the phenomenon, and the decisions students made when revising those models.Classroom observation notes help us improve the SageModeler user interface, the curriculum design, and teacher support materials, including teacher guides and professional learning workshops. We also plan to explore supporting teachers in professional learning communities and will collect feedback about what kinds of supports they need and how well the materials scaffold teacher practices.

Curriculum units

We are currently developing curricula in biology, chemistry, and Earth science. All curricular units are NGSS aligned and designed using project-based learning (Krajcik & Blumenfeld, 2006*), with a driving question around a phenomenon of interest to students. First, students experience or are introduced to the phenomenon and develop an initial model about the driving question. Then they explore key aspects of the phenomenon and revisit their model to revise, share with peers, and engage in classwide discussion about the various approaches other students have taken. Students compare the model output to lab data they have collected or to publicly available datasets. Throughout the unit, they have multiple opportunities to iteratively test, evaluate, and debug their system model in order to explain and predict the behavior of the phenomenon or to design a solution to a problem.

To research how different levels of modeling may scaffold students’ modeling practice and computational thinking skills, we are developing three types of units for each subject area: 1) a unit in which students develop a static model of the phenomenon, 2) a unit in which students develop a dynamic model, and 3) a unit in which students first model the phenomenon using a static modeling approach, then later transition that model to a dynamic version.

Our hypothesis is that moving from static to dynamic modeling may provide the stepping stones needed to make dynamic modeling accessible to more students. With a set of units that vary from using one type of modeling to using both static and dynamic, we hope to gain insights into what sequence of modeling experiences best supports growth in systems thinking, computational thinking, and system modeling. Developing these thinking and modeling skills is critical to the next generation’s ability to participate in STEM fields and design solutions for present and future complex problems.

* Krajcik, J. S., & Blumenfeld, P. (2006). Project-based learning. In R. K. Sawyer (Ed.), The Cambridge handbook of the learning sciences (pp. 317-334). Cambridge: Cambridge University Press.

Dan Damelin (ddamelin@concord.org) is a senior scientist.
Lynn Stephens (lstephens@concord.org) is a research scientist.
Namsoo Shin (namsoo@msu.edu) is an associate research professor at Michigan State University.

This material is based upon work supported by the National Science Foundation under grant DRL-1842035. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.