Navigating the World of Units in M2Studio
Fluency in dimensional analysis lays the foundation for a scientific mindset. It allows students to apply abstract mathematical concepts to understand physical phenomena. This foundation cultivates a disciplined approach to problem-solving, critical thinking, and analytical skills. Such competencies are crucial for informed decision-making and innovation in our increasingly data-driven world.
M2Studio is a web-based learning environment designed to make dimensional analysis more accessible and comprehensible as students create, troubleshoot, and refine mathematical models, empowering them to tackle real-world problems. M2Studio is built into our Collaborative Learning User Environment (CLUE) software and provides students with a dynamic graphic interface for building and visualizing their reasoning through text, drawings, images, tables, graphs, and flowchart-style diagrams. With a wide set of tools, it appeals to a variety of learning styles. Further, the multiple representations within the various “tiles” (text, diagram, etc.) are seamlessly linked to each other, helping students make connections across these representations.
Variable cards and mathematical expressions
Students use the diagram tile to create visual representations of their models. In M2Studio, the variable cards are a particularly powerful representation that foregrounds dimensional analysis. When creating a variable card, students can customize it by giving it a name and adding the unit, value, and notes (Figure 1). A variable (e.g., mass) is thus represented as a card in the diagram tile, which can be moved around and used to perform operations and build a mathematical model to represent and solve a problem. Students can link the variable cards to formulate and visualize complex expressions, such as the relationship between mass, volume, and density.
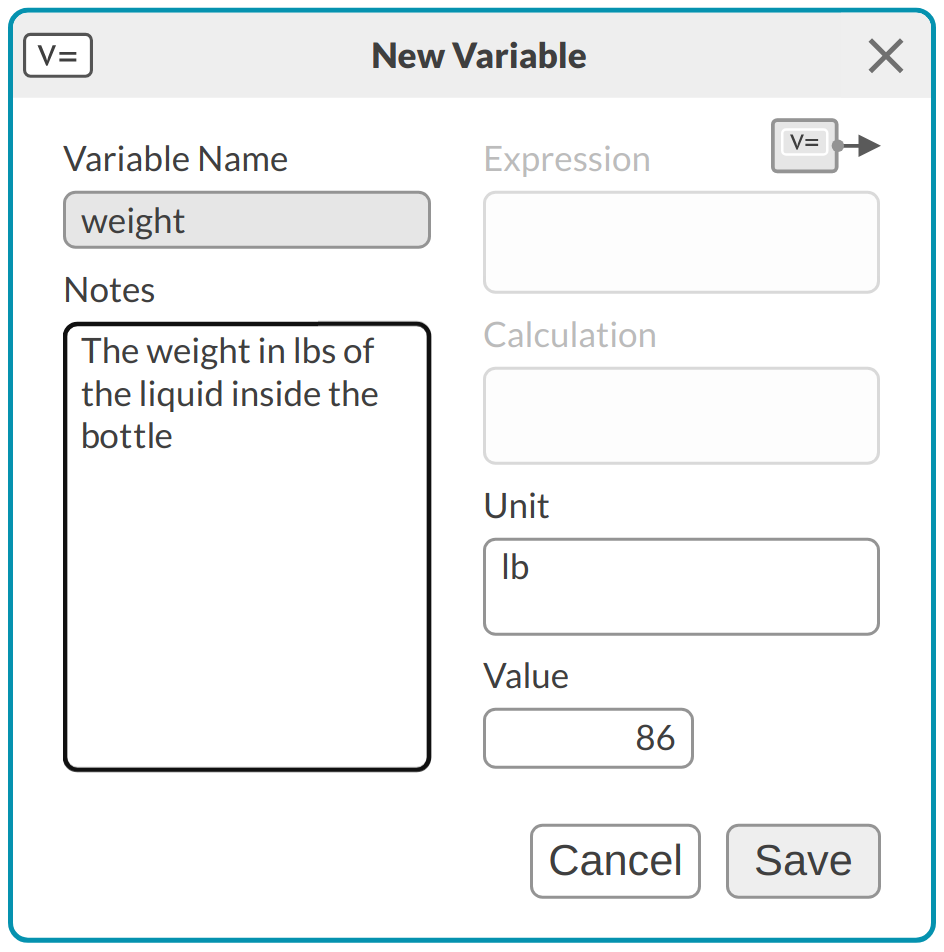
They create an empty variable card to represent the result of a mathematical expression (e.g., density in the expression density = mass/volume) and connect multiple input cards to it by dragging a connection line from the input variables to the output variable. They then write the mathematical expression in the appropriate field of that card, using the connected input variables’ names as well as numbers and operators. M2Studio automatically derives the units for the result, recognizing both singular and plural forms as equivalents (e.g., lb and lbs). It also allows students to mix different measurement systems as long as the units are equivalent.They can, for example, add miles to kilometers, and the result will be given in either system.These features reduce the friction of having to worry too much about spelling or navigating different unit systems, allowing students to focus on the modeling task.
M2Studio scaffolds student understanding
A unique feature of M2Studio is its handling of unit discrepancies. Students cannot simply choose the units resulting from a calculation to fit their expectations. Should students attempt calculations with incompatible units (e.g., adding pounds to cubic feet), the system highlights the error (Figure 2a). Students can then troubleshoot the units they used for the input variables and their mathematical expressions, delving into the “why” behind unexpected results. Was the error in the input units, the mathematical expression, or a misconception of the anticipated outcome unit? M2Studio instantly updates the model and final results to reflect any adjustments students make to the input variables and mathematical expressions. In addition, the output units can be converted to more appropriate ones (as long as they are compatible) by simply writing “in [desired unit]” (Figure 2b). This instant feedback mechanism fosters an iterative, discovery-led learning experience, invaluable for learning the principles of dimensional analysis.
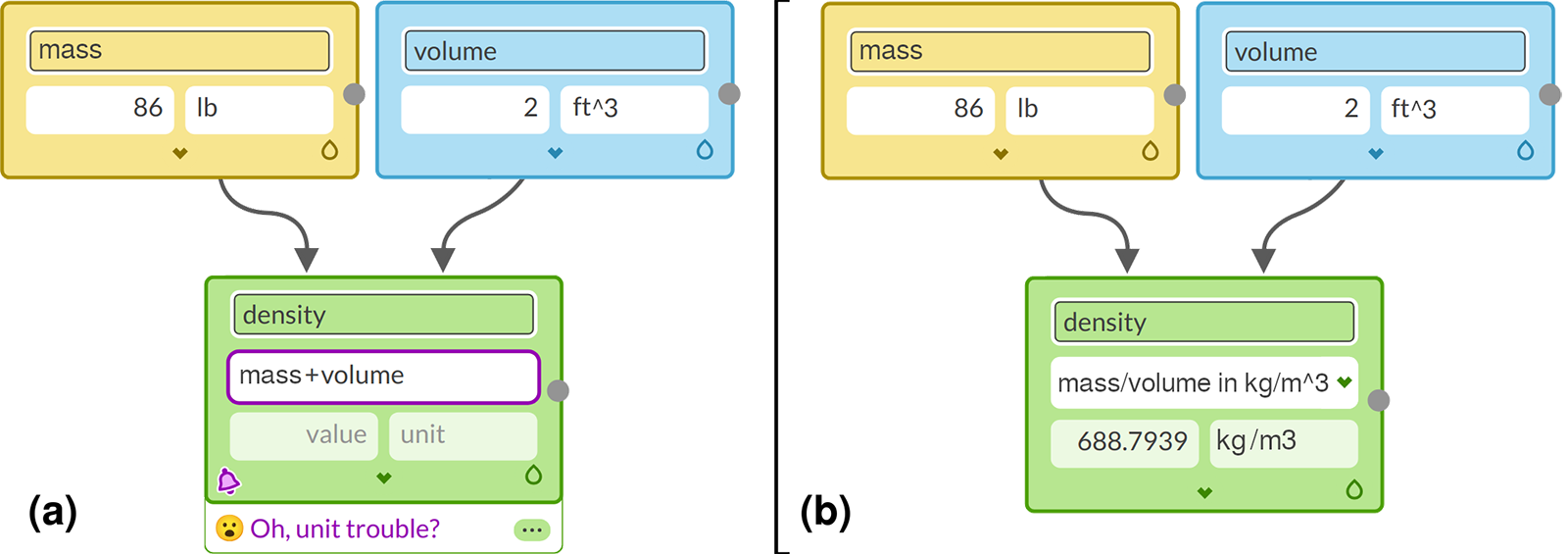
(b) The student corrects the expression and the result is instantly calculated.
An activity in M2Studio
The following activity showcases M2Studio’s practical application by engaging students in an immersive, real-world problem-solving experience. Students consider a pressing environmental issue and take on the role of an environmental analyst with a mission to tackle food waste. This exercise is inspired by a recent law passed in New York,* which mandates that businesses and institutions producing over two tons of food waste weekly must donate edible items and compost the rest.
Students are challenged to select a college and, using actual data (e.g., the number of resident and non-resident students, number of school days, etc.), estimate if the institution would comply with a food waste law similar to the one passed in New York. Equipped with only two key pieces of information—the two tons weekly limit and an average food waste estimate per student per meal**— students use M2Studio to create a mathematical model to solve the problem.To calculate the total weekly food waste, students create variable cards to represent the total number of meals consumed by resident and non-resident students and apply the average waste per meal (Figure 3).To create an effective model, students are steered to use units properly, naturally applying dimensional analysis.
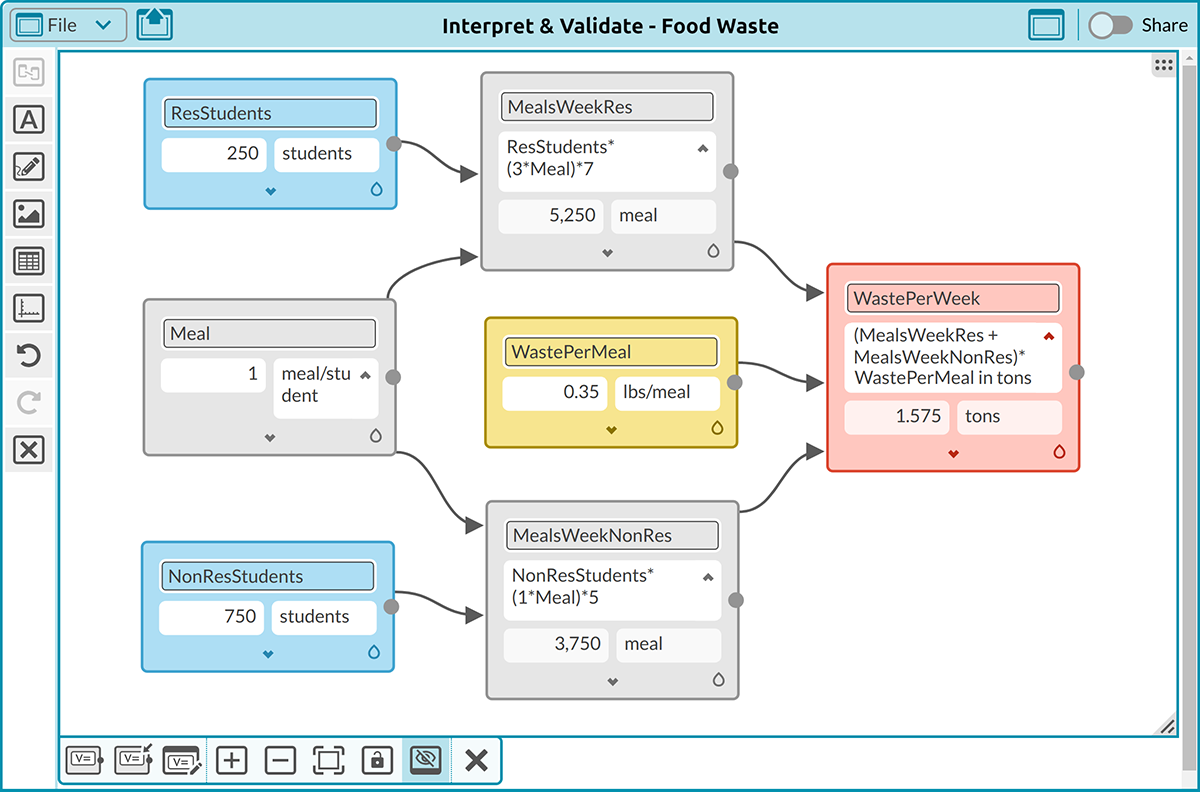
This exercise introduces the mathematical modeling process using variables with real-life implications, encouraging students to critically analyze their findings. For example, if their calculations show that their college would exceed the two-ton threshold, students might test which factors play major roles in food waste, evaluate strategies for waste reduction (e.g., establishing a ceiling for the number of resident students), or analyze the effects of different solutions. In this activity, teachers can deepen students’ engagement with the problem by considering a variety of outcomes and solutions or discussing environmental impacts.
Beyond numbers
M2Studio is designed to visually facilitate the troubleshooting of students’ mathematical models. Giving students instant feedback on unit appropriateness and providing automatic unit conversions allows students to take a dimensional perspective before adding numerical data, building models with variable cards that initially focus on units, even without associated values (Figure 4). The iterative process of building, testing, and refining models cultivates an analytical mindset, empowering students to explore various scenarios, incorporate new elements, and adapt their models to address broader questions. By prioritizing the structural integrity of their models—ensuring that units align and that their results are plausible in terms of units and values—students sharpen their analytical skills and abstract thinking, learning to conceptualize complex systems without the immediate need for numbers. By supporting dimensional analysis, M2Studio highlights the profound lesson that mathematics transcends numbers, revealing its nature as a language of patterns, relationships, and logical reasoning.

* https://www.nysenate.gov/legislation/laws/ENV/A27T22
** The average waste per meal varies widely depending on the types of meals served and the waste reduction strategies in place. Students use a single value as a first estimate to simplify the exercise.
Kenia Wiedemann (kwiedemann@concord.org) is a research assistant and project manager.
This material is based upon work supported by the National Science Foundation under Grant No. DRL-2101382. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.