Designing a Digital Collaborative Mathematics Classroom Using a Problem-Based Curriculum
For nearly three decades, the Connected Mathematics Project (CMP) has worked to design, develop, field test, evaluate, and disseminate student and teacher materials for mathematics classrooms. CMP was developed as a complete three-year, problem-based middle grades curriculum. CMP has been used by thousands of students across all 50 states and in many international schools, and has received multiple awards and accolades, including exemplary status by the U.S. Department of Education’s Mathematics and Science Education Expert Panel.
Since its initial publication in 1996, the goal of CMP has been to create a classroom environment that supports students’ mathematical development through the process of exploring, conjecturing, reasoning, communicating, and reflecting. When mathematics is embedded in contextual problems, the challenge for teachers is to pay attention to students’ problem-solving strategies, help them make the mathematics visible, and connect the embedded mathematics learning to prior and future understandings.
One of the key features in a CMP classroom is collaboration. Students and teachers actively work together on important and challenging mathematical tasks. In the Launch phase, the teacher connects the context to prior knowledge and describes the challenge. During the Explore phase, students work together to solve the problem as the teacher moves around the classroom observing, prompting, redirecting, questioning, and encouraging. Students make and validate conjectures, consider alternative strategies, question each other, and communicate their findings. In the Summarize phase, the teacher and students share, solidify, clarify, validate, generalize, connect, and extend their understandings.
New possibilities for CMP: Digital collaborative environments
While extensive research on CMP has shown increases in both student and teacher learning and dispositions towards mathematics, CMP authors continue to seek ways to enhance student and teacher learning. A recent grant awarded by the National Science Foundation to the Concord Consortium and Michigan State University explores new possibilities for CMP classrooms. The goal of the Digital Inscriptions project is to leverage the unique affordances of technology for 21st century learners and develop a digital collaborative CMP classroom that enhances student learning of mathematics. Could we build a “living” textbook where social and carefully structured math learning can promote true disciplinary engagement?
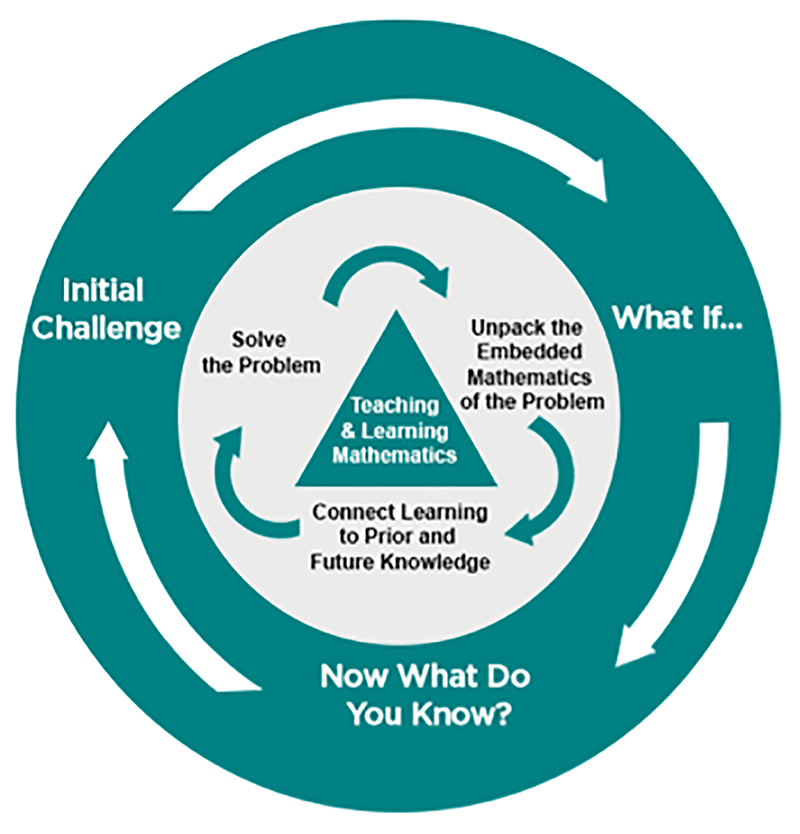
While envisioning a living textbook for today’s learners, we were inspired by STEM disciplines that focus on problem-solving, critical thinking, and collaboration. We wanted to promote learning that resembles the work of STEM professionals, so we redesigned the CMP problem format to more closely align with a STEM environment. The Initial Challenge contextualizes the problem while What if…? provides the opportunity to make the embedded mathematics visible. Students take ownership of their learning in Now What Do You Know? as they connect their learning to prior knowledge and consider future payoffs. The CMP STEM problem format for the digital environment continues to support the Launch/Explore/Summarize phases of the lesson (Figure 1). This framework also helps teachers address the challenge of teaching mathematics when the mathematics is embedded in problem contexts.
We also considered how to integrate the potential of digital media into existing CMP classroom practices. The new platform includes the following features.
Digital feature 1: Embedding student workspaces and mathematics tools into the textbook
In the CMP curriculum, learners immediately engage in doing mathematics within a situating challenge. The digital platform immerses learners in problem-solving that begins with the Initial Challenge and continues throughout the unit, culminating with students understanding key mathematical ideas embedded in the unit. To support a smooth transition to problem-solving, each problem has an embedded workspace adjacent to it. Elements of the problem (text, images, graphs, tables, etc.) can be dragged into the workspace where they are converted into special-purpose, interactive “tiles” that can be rearranged (Figure 2). Students have access to embedded digital tools to solve the problems, including tools for writing text and creating tables, images, drawings, and graphs. This flexible workspace allows students to dive into the problem using resources suggested by the problem, as well as other tools, to develop their own solution strategy. According to one student, “At my age people understand technology better than other things. Some people can’t draw and some people can’t write as well, but with technology it’s easier for everyone to type and draw with the computer.”

Digital feature 2: Transforming prior problems into reusable artifacts to support future work
As learners transition from the Launch phase of the problem to the Explore phase, they solve problems and scenarios by connecting and building on mathematical ideas they have developed when solving earlier problems. In the software adaptation of CMP, students can revisit workspaces from prior problems to review older artifacts and copy-paste them into new workspaces. This helps learners “remix” the mathematical formalisms they have used in the past, combining, for example, an equation developed in an Initial Challenge with a graph that uses the equation to solve a new What if…? problem. The reusable artifacts make concrete the CMP design principle that as learners encounter new situations in which they use mathematical reasoning, skills, and procedures, they make connections to ideas they have already encountered.
Digital feature 3: Transforming the textbook into a safe, shared collaborative workspace
What distinguishes experts in a domain from novices is not necessarily the amount they know, but the speed and accuracy with which they match what they know to the needs of the situation. CMP design guidelines state it this way: “knowing how to, but not when to, is not sufficient” for developing mathematical conceptual and procedural understanding. Far too often, students learn mathematics as a recitation of form. When given a problem framed in a particular way, they faithfully execute the solution steps by rote. Knowing what framing to use, however, is core to understanding. Novices can be “trapped” in their preconceptions about how to view a problem. Exposure to the thought processes of others can be helpful. In paper and pencil CMP classrooms, teachers adopt strategies, such as jigsawing, to help students “cross-populate” ways of thinking about a problem. Seeing a variety of ways to solve the same problem, learners are better able to attend to (and develop versatility with) problem framing, fundamentally changing their notion of what it means to “do” mathematics from mere process execution to a metacognitive level of mathematical reasoning.
One way the digital platform supports learners’ ability to flexibly frame problems is in the design of a “parallel awareness” view. When learners log in, they are assigned to groups of four. While working on problems in their individual workspaces, each learner accesses the so-called “four-up” view, which juxtaposes the learner’s workspace with those of the other three group members (Figure 3). At the click of a button, students can share their own work and see what their partners are doing in real time. They can also copy artifacts created by their teammates. One student remarked, “I can drag other people’s work and graphs into my workspace to help me solve the problem in a better way.” At the same time, this student was glad to share work she had done, noting, “It feels good when a student uses my work to help them on their own problem because it feels like I’m doing something for someone else, even though I’m just doing my own work.” Students can discuss strategies and assign parts of the problem to individuals, and then combine their strategies into a complete solution that can be shared with the class.
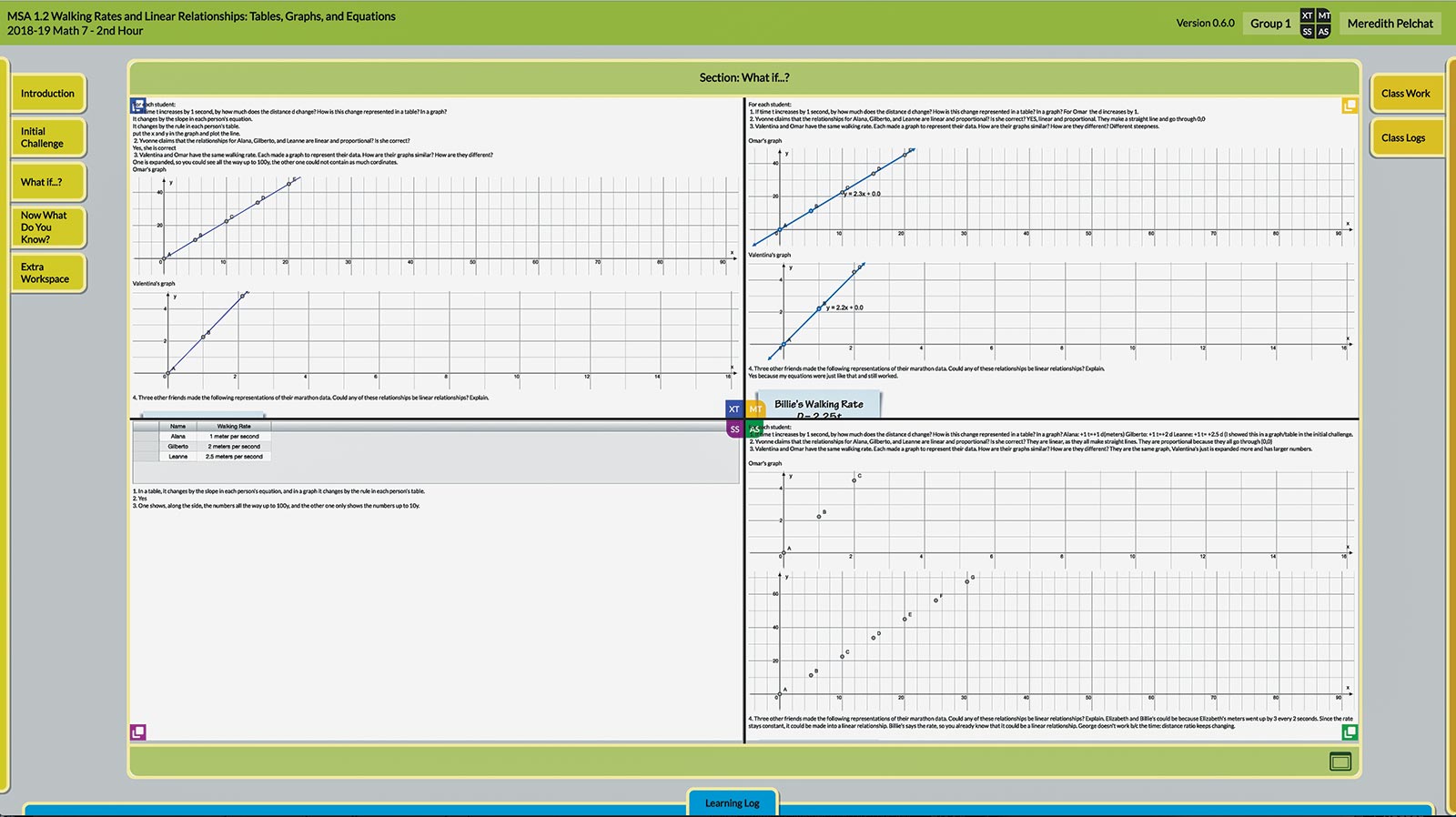
Being privy to one another’s problem framing, learners reflect on which approaches to the solution make the most sense. They revise their own strategies to use the best ideas, and practice the metacognitive skill of evaluating and choosing a problem frame. Another student said, “I can share my work and then I can talk to my partner and we can both get our ideas together to get one solid answer.” And according to the teacher, “If they’re stuck I often see them turn to the person next to them and say, ‘Turn on your sharing screen. Look at my screen and see if that gives you some ideas.’” She continues, “It’s safer than before when they would have to ask, ‘Can I see your notebook?’ It felt more like cheating when they were doing it paper and pencil. On the computer they’re comfortable letting each other see their work or share it.”
Digital feature 4: Extending and connecting the lifespan of concepts from textbook units
Reusable digital artifacts are more than a convenience. They allow learners to reuse concepts. During the Summarize phase, the class as a whole reviews and consolidates concepts, using the Now What Do You Know? question(s) as a prompt. The idea is that the classroom distills their shared knowledge into artifacts they can easily refer back to in future units, or even in future years of the curriculum. This allows learners to distribute their practice over time, helping them reach a level of fluency in familiar and unfamiliar situations, allowing them to make connections to other concepts and procedures. The digital environment consolidates concepts by streamlining the process of collecting, revising, and combining mathematical artifacts in a separate area intended to record crosscutting ideas, concepts, and procedures: the Learning Log. Students can copy tiles from curriculum materials, problem workspaces, the workspaces of classmates or the teacher, or prior Learning Log entries, and edit them to best capture the concept. They use these entries to pull together ideas into the sort of repurposable formalisms that make mathematics so useful. Learning Logs persist across problems and units, and potentially across academic years, allowing learners to revisit, reuse, and refine their mathematical insights throughout the CMP curriculum.
Mathematics for a social classroom
The new CMP digital platform builds on the strengths of the CMP classroom system, with its rich artifacts and culture of shared knowledge building, and re-envisions how collaborative teaching and learning in mathematics can be best supported. Placing artifacts at the center of students’ experience and making them readily accessible to all fosters idea sharing in ways that have never been possible before.
During the project’s pilot phase, the expressive and collaborative possibilities of this new platform have generated new insights among teachers who have taught with CMP for years. One teacher enthused, “Our students are used to being social on technology, so why not use those skills in our classrooms and allow them to be social on a technology about what they’re learning.” Making the textbook “come alive” is more than just making it interactive, it also makes it socially alive, integrated into the social fabric of the classroom.
Leilah Lyons (llyons@nysci.org) is an Associate Professor of Computer Science and the Learning Sciences at UIC, and Director of Digital Learning Research at the New York Hall of Science.
Elizabeth Phillips (phillips6@msu.edu) is a senior academic specialist in the Program in Mathematics Education at Michigan State University.
Chad Dorsey (cdorsey@concord.org) is President of the Concord Consortium.
This material is based upon work supported by the National Science Foundation under grants DRL-1620874, DRL-1620934, and DRL-1660926. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.