What Happens When Students Try to Work Collaboratively?
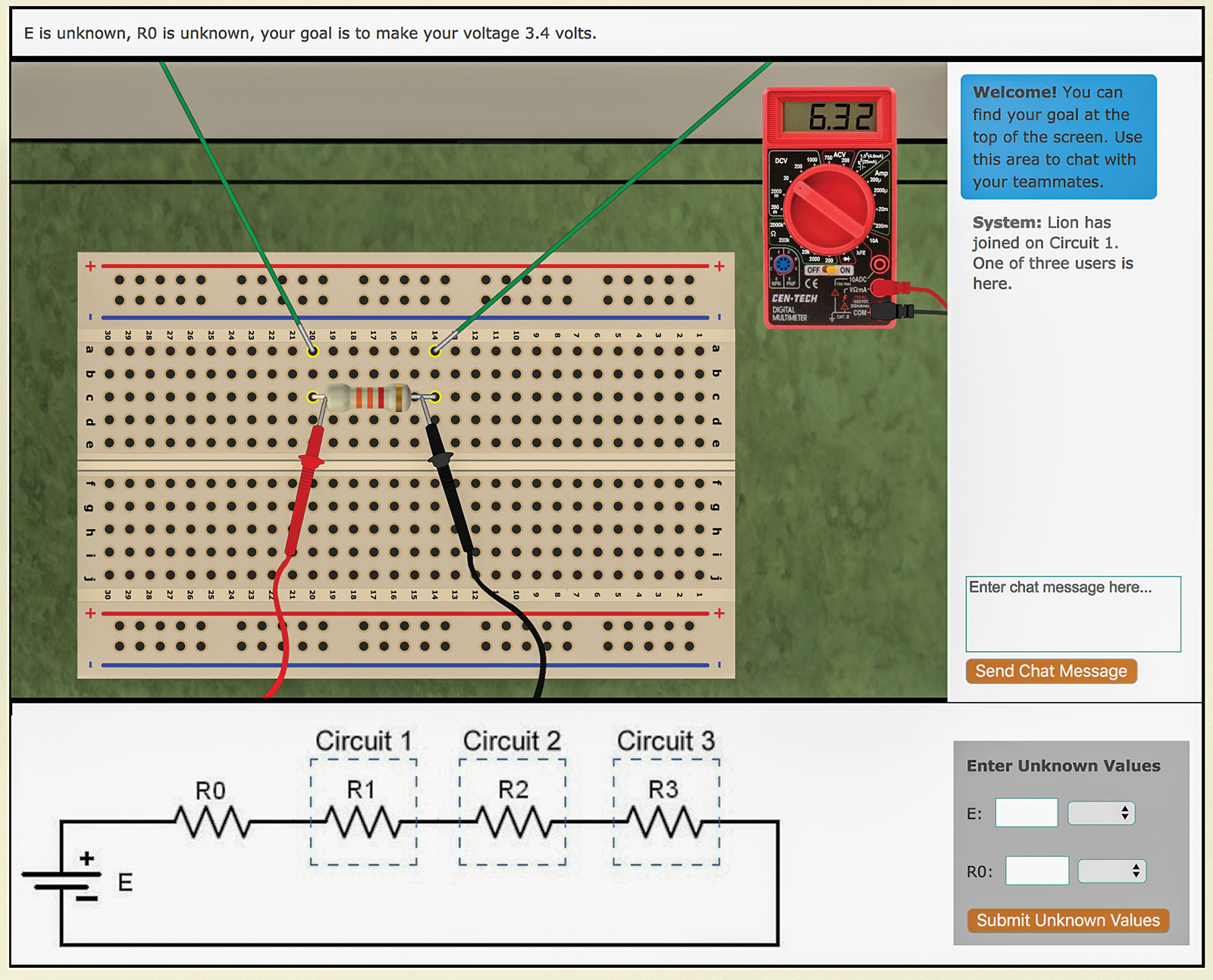
The problem is deceptively simple. The simulation consists of a variable resistor and a voltmeter with which to measure the voltage drop across the resistor. The resistor forms part of a larger simulated circuit, connected in series to three other resistors and a battery. The battery sends the same current through all four resistors, resulting in a voltage drop across each. Ohm’s Law states that those individual voltage drops can be calculated by multiplying each resistance by the current. The challenge for students: alter your resistance to achieve a specific goal voltage drop. Sounds simple, right?
To solve the problem, students click on their resistor, choose a new resistance from a drop-down list, check the voltage on the meter, then repeat until they get what they’re looking for (Figure 1). But there’s a catch. Those other resistors may not stay the same. Two of them are controlled by other electronics students, each of whom also has a goal voltage to attain and can alter his or her resistance to do so. The three must work as a team, each on their own computer and communicating only via a chat window. As described, their resistors are connected so that every time anyone changes their resistance, it affects the circuit as a whole and consequently changes the voltage drops of their teammates.
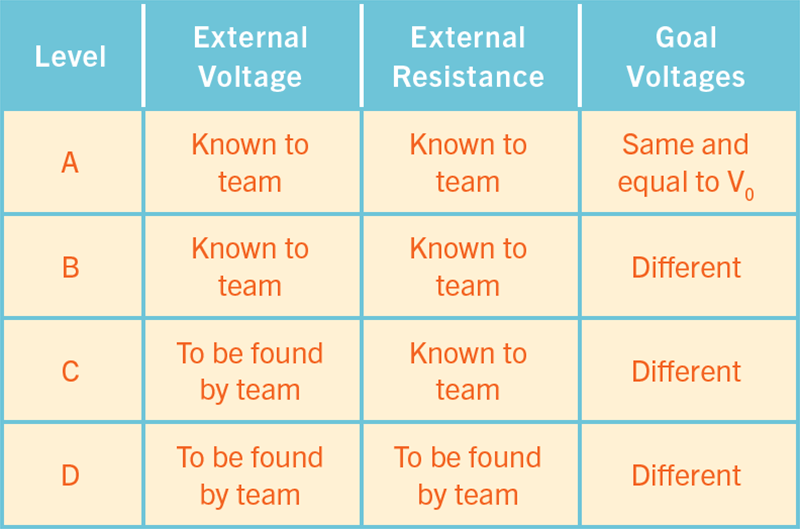
And what about the fourth resistance and the battery voltage? They cannot be altered by any member of the team, but they affect the behavior of the circuit. At early levels of the challenge, each team member is told the voltage and external resistance, while in later levels, they must compute them (Table 1). Each team member is provided with an online calculator and every calculation they perform, every circuit change, every measurement, and every chat message is monitored, logged, and analyzed by us.
Analyzing log data
The goal of the Teaching Teamwork project is to measure how effectively electronics students work in teams. We look for patterns in the data and try to answer questions, such as: do the team members collaborate or do they mostly work on their own? Are their actions coordinated or independent? Does a leader emerge to direct them? How does each member contribute to the ultimate success or failure of the team?
Take Team Birds, for example, three community college electronics students who attempted this challenge in March 2017. At Level A, we see from the log data that they succeed in achieving their goal voltage drops. Level A is the simplest: both the external voltage E and the external resistance R0 are known to the team members and their goal voltage drops are the same and exactly one fourth of E, meaning that the goal voltage drops across all four resistors are exactly the same. Thus, if they’re clever they can achieve their goal by simply setting all their resistors to be the same as R0.
Team Birds makes a total of 28 resistor changes on the way to achieving its goals, and the team members chat with each other 24 times. They make no use of the online calculator. From this cursory analysis, it would appear that they are simply changing their resistors (perhaps at random) until they arrive at their collective goal. But these simple measures conceal a more complex process.
For one thing, those 28 resistor changes are not equally allocated across team members. Eagle made 20 resistor changes, Seagull made 7, and Hawk made only one change. That seems unusual, particularly when you realize that the problem is very tightly constrained: for each voltage drop to match its goal, its resistance must be set to one and only one value. Moreover, the first student to do this is not rewarded with instant success. His voltage drop is not yet at the goal since the other two members of the team still have their resistances set “wrong.” In making only one change to the correct value, and then keeping it there, Hawk was either incredibly lucky or somehow knew what he was doing. What was going through his head?
We have only the log data to guide us. Hawk makes his momentous resistor change just over five minutes into the challenge. What does he know at that time? Everyone knows their own goal voltage drop, of course, and because this is Level A, everyone knows E and R0. From the record of chats we see that by the time Hawk makes his resistor change he has told the others what his goal is, has asked them for theirs, and has received a reply from Seagull but not from Eagle. Nevertheless, even with incomplete information, Hawk appears to know what his resistor should be in order to achieve the goal. And sure enough, 40 seconds after setting his resistor, Hawk asks, “Eagle, is your goal voltage also 2 V?” Eagle replies, “Yes,” and Hawk says, “So we all have equal voltages . . . so I think all of our resistors should be the same value as R0.”
Hawk has explicitly told the others what to do, but they ignore him and continue to make resistance changes intended to approach their goals, but—because they don’t both arrive at their goal voltages at the same time—missing each time. Finally, Hawk again urges his teammates to match their resistances to R0, and when, a minute later, Eagle finally does this, they achieve their goal.
At Level B the goal voltage drops for different students are all different, making the problem a bit harder, but Team Birds solves it in just over seven minutes. This time they make 23 resistor changes (again, only one by Hawk). They chat 14 times and make use of the online calculator 10 times.
Once again, Hawk seems to be the leader. He appears to know what his goal resistance should be, makes that one change, and then sticks with it, waiting for the others to catch up. Indeed, by analyzing his use of the online calculator, we can tell that he computes his goal resistance in a three-step process: he computes goalV0 as E – goalV1 – goalV2 – goalV3, then computes the goal current by dividing goalV0 by R0, and then finds his goal resistance by dividing his goal voltage by the goal current. This is basic Ohm’s Law math.
Hawk changes his resistor and then communicates the goal current to the others. They ignore this information, however, and continue to change their resistors without knowledge of what each of their goals should be. This goes on for two minutes, after which Hawk reminds them, “Unless we all have our appropriate resistor value in, the correct voltage will not display, though. Just to keep that in mind.” As it happens, he says this just as Eagle and Seagull converge to the correct resistance values— without actually calculating them. Then Hawk says, “Great job guys.”
A picture is now emerging: Hawk knows how to solve the problem, but doesn’t communicate that knowledge very effectively to his teammates, or perhaps he’s trying to teach them how to solve the problem, rather than “spoon-feeding” them the answers. Does he see this as “cheating”?
Misconceptions emerge
By Level C, the Birds know the routine—they communicate their goal voltages within the first minute, a good first step and indicator that they have the shared information to solve the problem. Then, about one minute in, Eagle notices something: “It looks like the voltage will step down with each circuit.” Let’s be clear. For this case the (randomly chosen) goal voltage drops for R1, R2, and R3 are, respectively, 4.11 V, 1.98 V, and 0.88 V. As Eagle points out, these happen to be in descending order. It’s a total coincidence, but it fits into a well-known misconception: that as the current travels around the circuit, the voltage is “used up,” so most of it ends up across the first resistor, leaving progressively less and less for the other two. There is no validity to this model, but it is pervasive among novice learners. In this case, it leads to disaster.
Eagle’s “discovery” leads Hawk to comment, “Oh yeah, you’re right. It halves down each time.” Well, not exactly, because 1.98 is not half of 4.11, nor is 0.88 half of 1.98, but close enough for Hawk to continue, “Well, that should make this a little easier since there’s a pattern.” They’ve found a pattern where there isn’t one and it will lead them astray for almost half an hour. After a few futile attempts at calculation, they fall back on a long, frustrating series of resistor changes interspersed with messages. At about 18 minutes, they achieve the goal—momentarily—but before they recognize and communicate that fact, one of them changes his resistor and they’re off to the races again. They finally get back to the desired state almost 10 minutes later, but it is clear from the chats that they have no idea how they did it.
At Level C the team is also asked to find E, the external voltage, and here Hawk’s expertise returns. He divides his voltage by his resistance to find the current, multiplies the current by R0 (which is known to all the team members at this level) to find the voltage across the external resistance, adds that to the voltages across the other three resistances and voilà—the sum is E. The entire process takes less than half a minute!
Hawk is capable of using Ohm’s Law in a relatively sophisticated strategy to find the external voltage. But having been led astray by a misleading pattern, all of his learning goes out the window when he tries to compute his goal resistance.
Finally, at Level D, the Birds are unable to attain the correct voltages at all. They try over and over with remarkable persistence, exchanging 98 chats and making 67 resistor changes (this time evenly distributed among the team members). Twenty-four minutes into the ordeal Hawk says, “Want to wrap this up?” Eagle replies, “Not yet. Let’s keep trying! We can do this.” Hawk, though, gives up on trying to get the right voltage and starts submitting various guesses for E, which he correctly surmises will be an integral value. After four tries, he guesses correctly. He then turns his attention to guessing R0, but after eight incorrect guesses he gives up.
Human cognition and the challenge of automated scoring
Human cognition is complex. This case study emphasizes how students cannot usefully be characterized as “knowing” or “not knowing” something. Does Hawk (or Eagle or Seagull) “know” Ohm’s Law? Clearly, context is everything. Team Birds is able to succeed at Level B in seven minutes, but struggles at Levels C and D where the voltage challenge is exactly the same. Hawk doesn’t suddenly lose his knowledge of Ohm’s Law at those levels, he just fails to apply it.
Imagine how difficult it would have been to automate the data analysis for this case. What would it take for a computer algorithm to detect the devastating and lasting effect of Hawk’s fruitless pursuit of a perceived pattern in the data? How can such effects even be accounted for by an assessment methodology that scores item responses under the assumption that they are independent? Gleaning useful information from logs of student actions is more akin to analyzing video data than it is to scoring their answers on a test. For the time being at least, it is a task best left to humans.
Paul Horwitz (phorwitz@concord.org) is a senior scientist.
This material is based upon work supported by the National Science Foundation under grant DUE-1400545. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.